
Tipping and switching
Life is a complex, interconnected web of small and large strategic situations. Our choices can affect the payoffs and choices that other people make. Choices of the group, likewise, can affect the payoffs and choices we make in turn. The strategic interdependencies between and within groups can produce an array of social phenomenon. This post is most interested in games of tipping and switching. In later posts, we’ll look at games of congestion, the tragedy of the commons, price competition, and games of spatial interdependence.
Tipping points
Some games may possess strategies that become more attractive the more players use it. We call this tipping (as opposed to congestion, in which a strategy becomes less attractive the more players use it). These games may also possess a tipping point. This is the critical mass or threshold of players that induce others to switch to the same strategy. Fashion trends provide a good example of tipping. As Malcolm Gladwell points out in The Tipping Point, new fads typically begin with a few early innovators. In fashion, these innovators might be celebrities or athletes. If the novelty is sufficiently sticky and contagious, then the fad may grow beyond early adoption. It may spread to followers, imitators and the eventual swarm.
Network effects and switching
Network effects are another example of tipping. This is where a good or service becomes more valuable to consumers as more and more people use it. Social media is a classic example of network effects in the technology industry. People find it hard, for example, to abandon Facebook or LinkedIn because everybody else is using it too. This is a powerful competitive advantage for the social media giants.
Case study: Skype or Zoom?
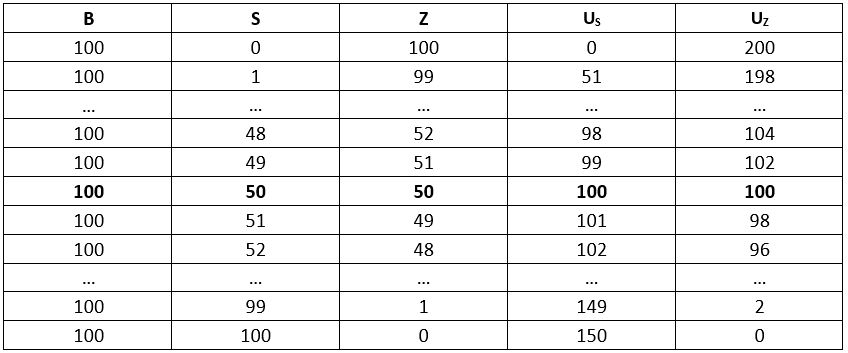
Let’s assume that there are one hundred businesses (B = 100) in this simple economy. They must decide between using Skype or Zoom for video calls. Let S represent the number of businesses that use Skype, and Z the number of businesses that uses Zoom, such that:
B = S + Z = 100
Payoffs
Next, let’s assume that Skype is more accessible to each individual user. Maybe it has a lot of snazzy features that users like. Zoom, by contrast, offers better connectivity and cross-business functionality. That is, Zoom becomes relatively more helpful when more businesses are using it for communications. Perhaps they make it easier to maintain large business networks. Let’s then assume that the payoff (U) to each business from using Skype or Zoom, based on the number of businesses using Skype (S) or Zoom (Z), is as follows:
Skype payoff:
US = 50 + S
Zoom payoff:
UZ = 2Z
What will businesses do in this game? Will they choose Skype or Zoom?
Best response
To solve this game, we must first look for their best response rules. Ostensibly, businesses will choose Zoom over Skype when the payoff associated with Zoom is greater than Skype. That is:
UZ > US
2Z > 50 + S = 50 + (100 – Z)
Z > 50
Nash equilibrium
In other words, if businesses believe that more than 50 businesses will use Zoom, then it is in the business’ best interest to use Zoom. To see why, it helps to think at the margins. If 50 other businesses use Zoom, and 49 use Skype, would you rather be the 51st Zoom user or the 50th Skype user? The former yields a payoff of 102, while the latter yields a payoff of 100. In this way, we can have a Nash equilibrium in which every business chooses Zoom. That is, there is no incentive to switch when everybody is using Zoom.
By contrast, if a business believes that less than 50 businesses will use Zoom, then the business prefers to use Skype instead. Again, to see why, it helps to think at the margins. If 49 other businesses use Zoom, and 50 use Skype, would you rather be the 50th Zoom user or the 51st Skype user? The former yields a payoff of 100, while the latter yields a payoff of 101. That is, we can also have a Nash equilibrium in which every business uses Skype – as there is no incentive to switch to Zoom when everybody is using Skype.
Tipping point
So, we can think of S = B = 50 as the tipping point of this game. If you look closely, the incentives that businesses face here are seemingly unstable. If S = B = 50, Skype users want to switch to Zoom, while Zoom users want to switch to Skype.* Where might the cards fall? We can’t really say without more assumptions about their beliefs. However, we can say that the strategic profile – in which 50 businesses choose Skype and 50 choose Zoom – is not a Nash equilibrium. At this profile, each business has an incentive to change their strategy.
*Skype users want to switch because being the 51st Zoom user is better than being the 50th Skype user. Likewise, Zoom users want to switch because being the 51st Skype user is better than being the 50th Zoom user. A situation in which S = Z = 50 is unstable since nobody is satisfied with their strategy. The game is likely to tip in one direction or another.
Game of tipping – Skype and Zoom players and payoffs
Self-fulfilling prophecies
The results above show that expectations and beliefs are important to strategic outcomes. The game tips into one direction or the other based on the beliefs that businesses form about everybody else. If consumers expect everyone to use a product with network effects, then they’re likely to switch to that product too. Expectations can become a self-fulfilling prophecy. For such beliefs to form, common knowledge is a helpful property. This is why companies spend a lot of money to advertise at mega events like the Superbowl. Not only do companies want everybody to know about their products, but they want everybody to know that everybody knows that their products are desirable. If successful, this mix of common beliefs, network effects, and economies of scale, can provide a self-reinforcing runway to market dominance.
Market size matters
Market size, in addition to expectations, is important for products that depend on network effects. To see why:
US > UZ
50 + S > 2Z
S > 2Z – 50
If S = 0, then US > UZ if Z < 25
Intuitively, if the total number of businesses is less than 25, then the payoff from using Skype is always greater than using Zoom. Here, there is only one Nash equilibrium in which everyone uses Skype. The market simply isn’t large enough for Zoom to generate sufficient network effects to pry users away from Skype.