
What a stylised political race and competition for voters can teach us about spatial interdependence, strategic positioning, and the propensity for convergence and divergence.
The political race
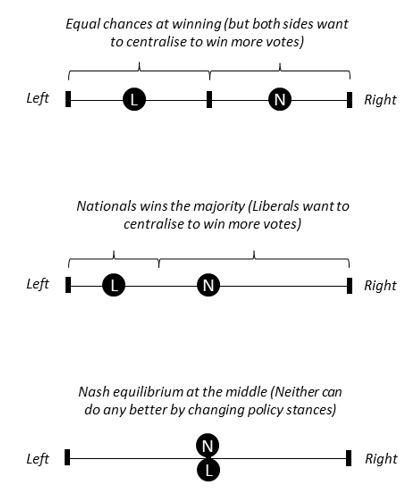
In this game, two candidates, a National and a Liberal, compete for the presidency. Each candidate must choose a policy stance. We have the far left (L) on one hand, and the far right (R) on the other. Candidates must choose one of these extremes, or somewhere in between.
To win the election, the candidate must receive the majority of votes. In this simple political economy, let’s assume that voters are distributed evenly across the political spectrum. We assume also that voters will vote for the candidate that aligns most closely with their political ideology. If both candidates are politically equidistant, then voters will choose either candidate with a 50 percent chance.
Let’s assume also that each candidate cares only about winning office. What political stance will each candidate take?
Nash equilibrium
The unique Nash equilibrium of this game is for both candidates to take a centrist position. That is, to take a policy stance that represents the political ideology of the median voter. To see why, let’s consider the best response of the National when the Liberal takes a centrist position.
If the National takes a left leaning or right leaning position, the Liberal will win the majority of votes. But by taking a centrist position, the National can retain a 50 percent chance of winning. Because this game is symmetric, the Liberal has the same best response when the National takes a centrist position.
Now, there is also no Nash equilibrium in which either or both candidates take a non-centrist position. For example, if a Liberal takes a non-centrist position, then the National’s best response is to take a more centrist position to win the majority. Increasing centrism continues until we converge upon the original Nash equilibrium once again.
A game of positioning (political race)
Convergence
The strategic situation in this simple political economy results in political convergence. Both candidates have a dominant strategy to take a centrist position. Of course, we don’t always see this behaviour in real life. Why? There are many potential reasons.
Firstly, political views are not evenly distributed. Nor are they distributed across simple dimensions from left to right. People have multifaceted wants that ebb and flow with time. Some positions may galvanise a subset of voters, whilst alienating another. Politicians make trade-offs on the votes they can and cannot win.
Secondly, I like to believe that politicians care about more than winning. Some, I hope, have a direction for their nation. Their task in part is to persuade people that their vision is worth voting for. The equilibrium to the game above assumes that politicians acquiesce to the whims of the majority.
Thirdly, voter preferences are not independent of the candidate. As social creatures, our beliefs and preferences are very much interlinked. Perceived charisma, authority, and likeability, introduce additional complexities to preferences, choice, and positioning.
Fourthly and relatedly, informational advantages may play a role. If the newcomer’s brand is nothing new or exciting, voters might find it safer to vote for the incumbent. After all, they know what they’re going to get. In this way, newcomers might seek a differentiated position to win over voters.
Spatial interdependence
While some positional games might result in convergence, others may lead to divergence. For example, groceries tend to fan out for the convenience of their patrons, and to minimise head-to-head competition. By contrast, luxury retailers tend to congregate at a centre or street. Co-location, in this example, adds to the shopping experience, and is convenient for customers that want to browse. Complementary effects in the luxury retailer game leads to convergence.