Sensitivity, Uncertainty, and Incompleteness — Brief notes on Clockworks, Chaos, and Computation

AuthorAthenarium / Posted on

Sensitivity, uncertainty, and incompleteness — Brief notes on clockworks, chaos, and computation

Of clocks and chaos

Nineteenth century mathematician Pierre Simon Laplace believed in a clockwork universe. He suggested that a supreme calculator, armed with Newton’s laws and the knowledge of every initial condition, could plot the course of the future. But, as Melanie Mitchell describes in her wonderful book Complexity: A Guided Tour, two discoveries in the twentieth century upended this mechanistic Newtonian worldview.

Quantum worlds

The first was the development of quantum physics. Werner Heisenberg’s uncertainty principle states, Mitchell writes, “that one cannot measure the exact position and the momentum (mass times velocity) of a particle at the same time”. That is, the more we know about the location of a particle at some time, the less we can know about its momentum, and vice versa. The behaviour, as strange as it seems to us macro creatures, reflects an uncertainty that is fundamental to the quantum world.

“Given the basic law and the initial condition, the history of the universe is by no means determined, because the law is quantum mechanical, thus yielding only probabilities for alternative histories. Moreover, histories can be assigned probabilities only if they are sufficiently coarse-grained to display decoherence. Thus quantum mechanics introduces a great deal of indeterminacy.”

Murray Gell-Mann. (1995). What is Complexity?

Butterfly effects

It is true, however, that quantum effects are less obvious on the scales of everyday living. Indeed, Newtonian physics provides a decent approximation of most things to this day. But there is a second challenge to the Newtonian world order: complexity and chaos. As meteorologist Edward Lorenz discovered in the 1960s with his weather simulations, tiny perturbations in approximations can lead to wildly different predictions. The issue here is twofold: nonlinear dynamics and sensitive dependence on initial conditions.

As Lorenz writes:

“Two states differing by imperceptible amounts may eventually evolve into two considerably different states… If, then, there is any error whatever in observing the present state — and in any real system such errors seem inevitable — an acceptable prediction of an instantaneous state in the distant future may well be impossible… In view of the inevitable inaccuracy and incompleteness of weather observations, precise very-long-range forecasting would seem to be non-existent.”

Edward Lorenz. (1963). Deterministic Nonperiodic Flow.

Many body problems

Even long-range predictions of planetary orbits, given their gravitational effects on one another, may vary greatly with minor changes in starting points. This is the nonlinear many-body problem of celestial mechanics. As Mathematician Henri Poincaré, who recognized the butterfly effect in the three-body problem, writes:

“If we knew exactly the laws of nature and the situation of the universe at the initial moment, we could predict exactly the situation of that same universe at a succeeding moment. But even if it were the case that the natural laws had no longer any secret for us, we could still only know the initial situation approximately… It may happen that small differences in the initial conditions produce very great ones in the final phenomenon. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.”

Henri Poincaré. (1914). Science and Method. Translated by Francis Maitland. In Melanie Mitchell (2009). Complexity: A Guided Tour.

Logistic maps

Indeed, even seemingly innocent but nonlinear equations like the logistic map (where xt+1 = R * xt * [1 — xt] ) can generate varied fixed-point, periodic, and chaotic (or strange) behaviours with different initial conditions and parameters. The animation below, for example, shows the behaviour (left chart) and frequency spectrum (right chart) of a logistic map for different parameter values (2 ≤ R ≤ 4) and initial condition (x0 = 0.5). If such varied behaviours can emerge from simple formulations, what then should we make of our complex world? 

Logistic map example

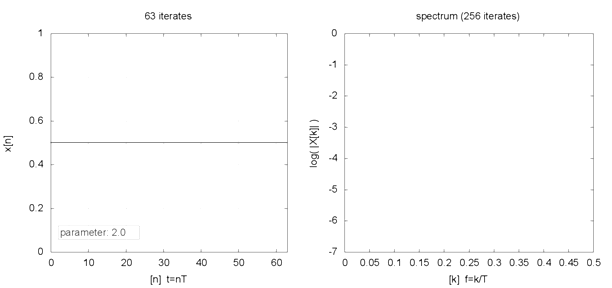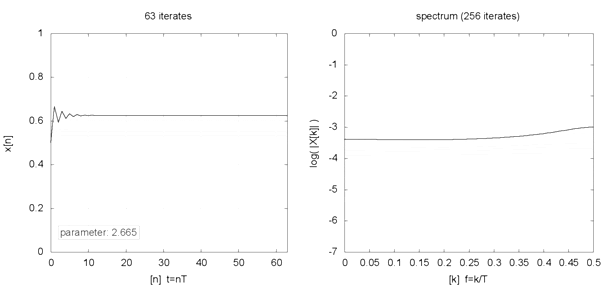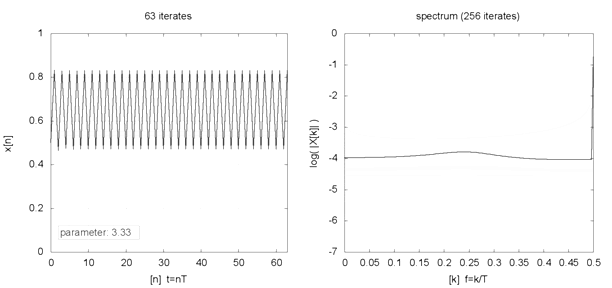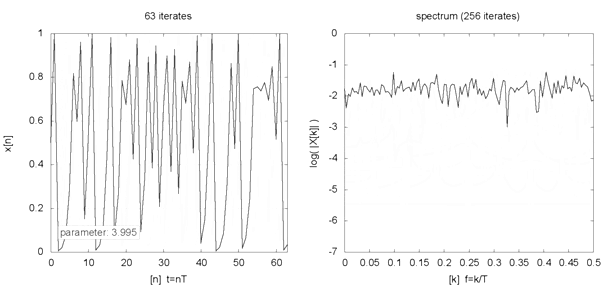
Source: Logistic map animation, Snaily. (2014). Wikipedia Commons.

Tiny world models

Uncertainty and sensitivity has broken Laplace’s conception of a mechanical universe. We can, of course, set ourselves a more humble task: to make rough predictions of tiny world models. We must wonder then whether our characterization of the system is reasonable. Are better models, data, and abstractions all we really need?

“Whenever a good [scientist] examines a simulation, [he or she] must wonder what bit of reality was left out, what potential surprise was sidestepped. [Albert] Libchaber liked to say that he would not want to fly in a simulated airplane — he would wonder what had been missed. Furthermore, he would say that computer simulations help to build intuition or to refine calculations, but they do not give birth to genuine discovery.”

James Gleick. (1997). Chaos: Making a New Science.

Nonlinearity is only one of the many ways in which physics can impose unexpected consequences on us. We’ve discussed previously, for example, how the geometry of scaling might constrain the structure of living and social systems. But I’d like to turn briefly now to another seminal discovery in mathematics.

Incompleteness theorems

In the early twentieth century, mathematician David Hilbert posed a problem to his academic community: to show that the axioms of arithmetic are consistent (or free of contradictions). Some three decades later, logician Kurt Gödel provided a hint with his ground-breaking incompleteness theorems. 

As Natalie Wolchover writes in How Gödel’s Proof Works, Gödel “proved that any set of axioms you could posit as a possible foundation for math will inevitably be incomplete; there will always be true facts about numbers that cannot be proved by those axioms”. What’s more, Gödel “showed that no candidate set of axioms can ever prove its own consistency”.

Now, the proof is quite involved.* But its essence, Wolchover explains, involves devising a numbering and mapping procedure that “allows a system of axioms to talk cogently about itself”. The trick then is to find a mathematical expression that is equivalent to saying “this statement is not provable”, much like the Liar’s Paradox. Indeed, proving that such a statement is true or false is contradictory. This in turn suggests that the arithmetic system that gives rise to such a statement “is either inconsistent or incomplete” (Mitchell 2009).

Inspired in part by Gödel’s proof, Alan Turing used a similar mix of self-reference and proof by contradiction to answer Hilbert’s Entscheidungsproblem just a few years later in 1936. In short, as Mitchell describes in Complexity, Turing showed that “not every mathematical statement has a definite procedure that can decide its truth or falsity”.

* For more on Gödel’s Proof, I recommend Gödel’s Proof by Ernest Nagel and James Newman, and Gödel, Escher, Bach, by Douglas Hofstadter.

Deep limits and hidden structures

Where quantum and chaos probe at clockworks, Gödel, Turing, and other great thinkers raise fundamental questions about the completeness, consistency and decidability of mathematics and computation itself. While everyday human experience is unlikely to test these profound limits, I cannot help but feel awestruck by their implications.

But I’ll cut this post short, somewhat deficiently and incompletely (bad pun intended). I only want to remind you of the uncertainty, sensitivity, and incompleteness that moves us all. Human understanding has come a long way since Laplace’s time. What else, I wonder, hides in the structural depths of reality and possibility?

Sources and further reading

Recent posts