
Move orders matter
Sequential game theory has contributed to our understanding of first mover and second mover advantage. Is it better to go first or second? To be a hare or tortoise? Unsurprisingly, it depends on the game, players, available strategies, move orders and associated payoffs.
First mover advantage in games of chicken
In a previous post, we showed that a simultaneous Game of Chicken – where two motorists, on separate ends, are racing headfirst towards one another – has two Nash equilibria in pure strategies: one player stays the course, while the other swerves away. Any other strategic profile in pure strategies is unstable. If both players stay then course, then both players want to swerve away. After all, nobody wants a fiery collision. Likewise, if both players swerve away, then both players want to stay the course.
Game of Chicken (Fast and Furious)

But in the sequential variant of the Game of Chicken, there is an obvious first mover advantage. Let’s say Brian is the reactive second driver. If he knows that Dom is staying course, he will want to swerve away. And if Dom is swerving away, Brian will stay his course. Knowing this, Dom, as the proactive first driver, will stay his course to earn his highest payoff (at Brian’s expense). This is the subgame perfect Nash equilibrium of the game.
Sequential Game of Chicken (Fast and Furious)
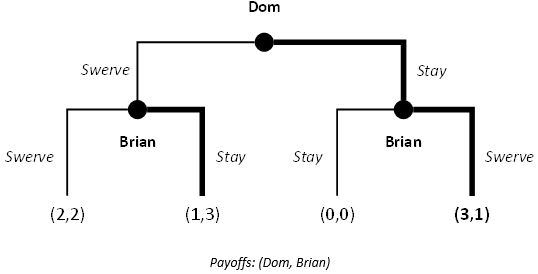
In sequential Games of Chicken with perfect information, it pays to move first. This then raises a question as to how to transform the game. Maybe Dom can make an irreversible commitment, to reach a point-of-no-return before Brian does. Variants of this game sees Dom removing his steering wheel and making this commitment known to Brian as well. Assuming Brian is rational, he should incorporate this information and swerve away.
Market expansion
The first-mover advantage is present in many real-life games. In some games of market expansion, for example, firms try to expand quickly to discourage others from market entry. If both firms enter and scale, they over commit and experience net losses. But if both firms exit, the other wants to enter and scale.
Game of market expansion

In the simultaneous game, there are two Nash equilibria in pure strategies in which one firm exits and the other scales. In the sequential game below, the subgame perfect Nash equilibrium sees: Shell exit if Aramco scales, and scale if Aramco exits; and Aramco scales given Shell’s best response. In the sequential game, first-mover Aramco guarantees its highest possible payoff.
Game of market expansion

Second mover advantage in games of pure conflict
The examples above illustrate the potential benefits of moving first. In the Game of Chicken, an irreversible commitment can force the second mover into the first mover’s most favourable strategic outcome.
But this is not true of all games. Sometimes it pays to move second. In the most extreme but simple of examples: A sequential game with perfect information for pure conflict games like Rock-Paper-Scissors or penalty kicks completely trivialises it. The second mover will always select the winning play.
Is it no wonder why businesses, militaries and nations pour tremendous resources into intelligence? Somewhat ironically, this desire for a second mover advantage might generate a secondary Prisoner’s Dilemma. This is where everybody is investing in intelligence and counterintelligence to no relative advantage.
First mover advantage in chess
Games of pure conflict may not always exhibit a second mover advantage. Consider the zero-sum game of chess for example. At the Grandmaster level, games are drawn about half the time. But players that play as white (the first mover) tend to win twice as much as those that play black (the second mover).
According to former Grandmaster Garry Kasparov, tempo is valuable in chess. And every sliver of advantage matters a great deal at the highest levels. The player that moves first is more likely to land the first successful attack. That is often enough to tip the winning odds in their favour.
Of course, chess is nothing like introductory game theory. There are far too many permutations to evaluate exhaustively. Indeed, players often rely on principled theories to develop their relative advantage. Former Grandmaster Yasser Seirawan, for example, emphasised the importance of force, time, space and pawn structure. At the risk of over-analogising, there may be general strategic applications to that.
What game are we even playing?
Sometimes, it’s not so clear whether a game confers a first-mover or a second-mover advantage. In business, is it better to release your product first to gain market share as quickly as possible? Or is it better to learn from the first-mover’s mistakes and to strike with greater innovation and improvements? There’s a similar parallel for investors, too. Should I invest in this start-up or IPO while it’s young and small, but information is scarce and its track record unproven? Or should I wait and see when there’s greater certainty, but likely at a higher price if the company does prove successful?
Further reading
- Nash equilibrium — A fundamental solution concept, and the hallmark of game theory
- Sequential games and subgame perfect Nash equilibrium
- Game of preemption and attrition — Impatience and inaction
- Commitments, threats, and promises — Tools to deter and compel
- Brinkmanship and the manipulation of shared risk