
More stags, more hunts
Recall that a sequential game (or extensive form) game specifies the sequence of decisions that players can make, the information they have when making decisions, and the payoffs associated with their path selection. In this post, we want to find solutions to sequential games. To do so, we introduce backward induction and subgame perfect Nash equilibrium (SPNE) – important additions to the game theorist’s toolkit.
Skip ahead
- Sequential stag hunts and strategy
- Subgame perfect Nash equilibrium (SPNE)
- The process of backward induction
- Move orders matter
Sequential stag hunts and strategy
Let’s consider, for example, a sequential variant of the classic Stag Hunt game. In this game, two hunters, Yosemite and Elmer, must decide between hunting hares or stags. While hunting stags yield a higher payoff, it requires coordination. Hunting hares, by contrast, is an individual activity that guarantees a smaller payoff.
In this game, Yosemite moves first, and Elmer second. It is also a game of perfect information and common rationality. That is, both Yosemite and Elmer know exactly where they are in the game and what has happened. They also know that each of them will pursue actions to maximize their personal payoffs. We summarize the decision tree as follows:
Sequential Stag Hunt Game
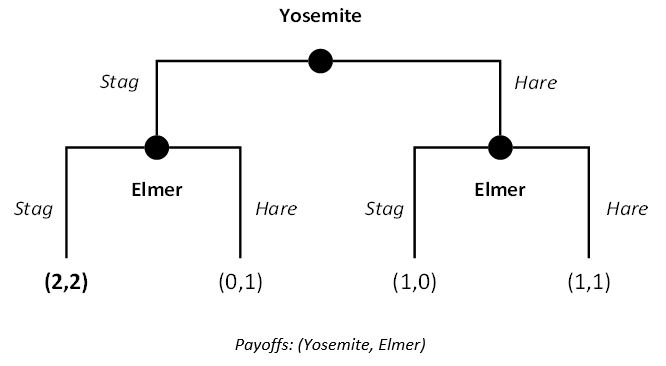
Strategy in extensive form games
How might players behave in this game? Remember, that to describe a strategy for a sequential game of perfect information, players must specify an action at every decision node. In the Stag Hunt game, Yosemite has two possible strategies: Stag or Hare. Elmer, by contrast, has four potential strategies as the second mover. He can: (1) always choose Stag; (2) always choose Hare; (3) choose Stag if Elmer chooses Stag, and Hare if Elmer chooses Hare; or (4) choose Hare if Elmer chooses Stag, and Stag if Elmer chooses Hare.
Subgame perfect Nash equilibrium (SPNE)
So what then is the solution to this sequential game? The solution concept we use is called the subgame perfect Nash equilibrium (SPNE). Firstly, recall that for simultaneous games, we have a Nash equilibrium (NE) when every player is using their best response. That is, for a given strategic profile, no player has an incentive to change their strategy. The SPNE is a more demanding version of the NE. For games with perfect information, a SPNE describes the strategic profile that sees every player use their best response at every decision node (even if those paths do not materialize under equilibrium). Put another way, a strategy profile is a SPNE if the sub-strategies constitute a Nash equilibrium at every subgame.
Subtrees and subgames
For clarity, a subtree, beginning at some non-terminal node, consists of that node and all subsequent nodes and branches that follow it. Subgames then include the payoffs associated with each subtree. Thinking in terms of subtrees and subgames can help us to solve the overall game. In our sequential Stag Hunt example, there are three subtrees.
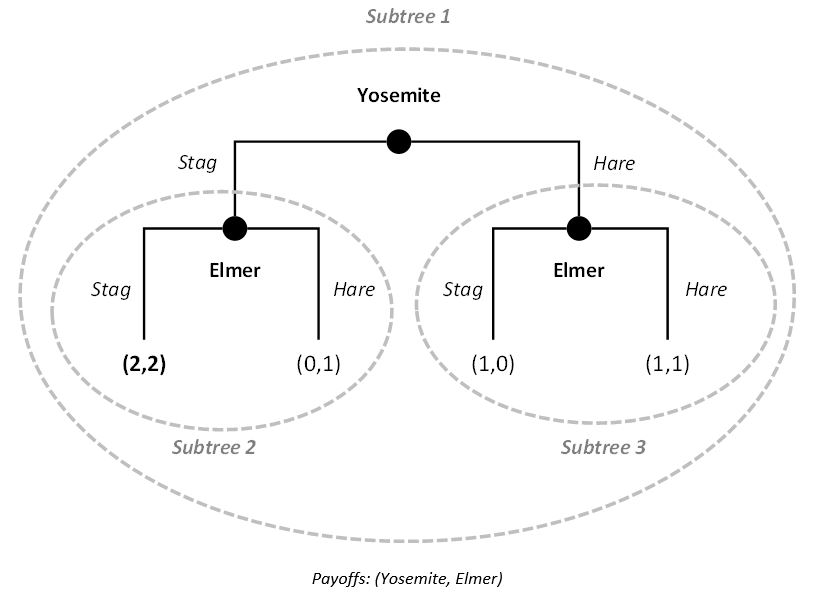
The process of backward induction
To find the SPNE of a sequential game, we use the process of backward induction. This involves ‘pruning’ the decision tree for optimal branches in two recursive steps. Firstly, you identify the player’s best response at the final (smallest) subtrees. The payoffs associated with the best response at each subtree then becomes the payoffs of the parent subtree. We then repeat steps one and two on the simplified (or ‘pruned’) parent tree. And we repeat the process over and over again until we arrive at the original decision node.
In the Stag Hunt game, we commence backward induction at Subtree 2 and 3. In Subtree 3, Elmer chooses Hare because it returns a higher payoff. But in Subtree 2, Elmer chooses Stag over Hare for a higher payoff. Yosemite foresees this and associates the best response payoffs of Subtree 2 and 3 with his decision node at Subtree 1. Because the payoff to Yosemite at Subtree 2 is higher than Subtree 3, Yosemite will choose Stag.
Indeed, the SPNE to this game sees: Yosemite choose Stag; and Elmer choose Stag if Yosemite chooses Stag, and Hare if Yosemite chooses Hare. The path trajectory that materializes in this game has both Yosemite and Elmer choosing stag. The payoff associated with the SPNE is 2 to both players.
Sequential Stag Hunt Game
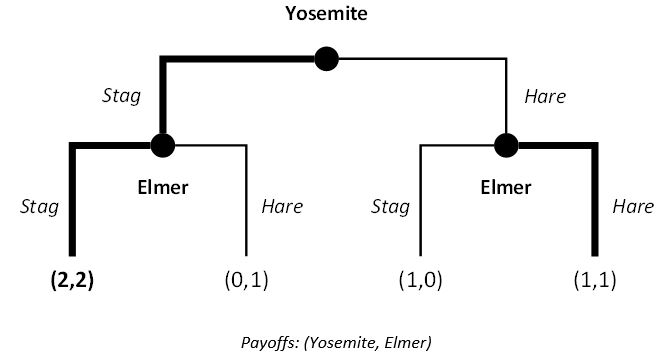
Move orders matter
In a previous post, we showed that the simultaneous Stag Hunt game has two Nash equilibria in pure strategies. If one hunter goes for stag, it is in the other’s best interest to go for stag too. But if one hunter goes for hares, then it is in the other’s best interest to go for hares too. But we cannot say which of the two NE solutions would result in play without more information.
Stag Hunt Game

In the sequential Stag Hunt game, there is only one SPNE solution. A sequential order trivializes this game of coordination because Yosemite knows that Elmer will choose what he chooses, Yosemite is happy to choose Stag to maximise his payoffs. Taking turns helped Yosemite and Elmer to achieve the best outcome.
One insight from extensive form games is that move orders can matter. Sometimes, the advantage goes to those that move first. On other occasions, it pays to go second. While the SPNE solution to this Stag Hunt game is intuitive, backward induction is most useful in solving complex sequential games. In a later post, we use backward induction and the SPNE concept to understand games of preemption and attrition.
Further reading
- Nash equilibrium — A fundamental solution concept, and the hallmark of game theory
- First mover and second mover advantage — Games of hares and tortoises
- Game of preemption and attrition — Impatience and inaction
- Commitments, threats, and promises — Tools to deter and compel
- Brinkmanship and the manipulation of shared risk
- Nash equilibrium in mixed strategies — Unpredictability in games of pure conflict