Extensive and normal form games – The structure of strategic situations

Sequential and simultaneous games

We can use game theory to model strategic games of interdependence. To do so, we must first develop a simplified description of reality. The description or structure of these games tends to distinguish between: (1) extensive form games, where actions happen sequentially; and (2) normal form games, where actions happen simultaneously. In this post, we want to focus in specifying the game. We’ll develop solutions for extensive (sequential) games and strategic (simultaneous) games in later posts.

Skip ahead

Specification, diagnosis and solution
Extensive form (sequential) games
Strategy for strategic situations
Possibility, permutation, and edge
Information, history and recall
Normal or strategic form (simultaneous) games

Specification, diagnosis and solution

Firstly, strategic situations should specify the players and their preferences, beliefs, choices, and knowledge. Recall also, that introductory courses assume that preferences are complete and transitive. That is, we can express the preferences of players as payoffs or utility.

Secondly, I want to emphasize how important it is to specify the game correctly. Consultancies and policymakers today are quick to diagnose the problem, believing that their time is better spent on deriving solutions. Remember that if you specify the game incorrectly, you’ll solve for the wrong problem.

Can you imagine if doctors prescribed medications before examining their patients? Or if an aircraft took flight before all the satisfactory checks? Unfortunately, this problem is rife in business because the consequences of malpractice aren’t immediately clear. As Richard Rumelt wrote in Good Strategy / Bad Strategy, take your time to understand and diagnose the situation.

Now, let’s begin with the structure of games.

Extensive form (sequential) games

Extensive form games are strategic situations in which players take actions sequentially. A game of chess, for example, is a classic extensive form game. In business, a company might introduce a new product. Their competitor, upon seeing this, decides on its response. That’s another sequential game.

Decision trees and nodes

Extensive games must describe the sequence of decisions that people make; the information they have when making decisions; and the payoffs associated with their interactions and path selection. We tend to represent extensive form games as decision trees. Each decision node, or dot on the decision tree, represents a choice that the player has to make at that moment of the game. Branches from each node describe how the game evolves as players make their decisions. After every player exhausts their successive decisions, the terminal or final node specifies the payoffs (or utility) that each player receives.

Example of a decision tree (Stag Hunt)

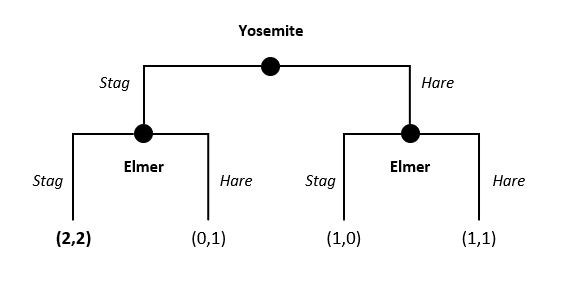
The decision tree above is an example of a sequential game between two hunters: Yosemite and Elmer. Yosemite, the first mover, decides between hunting stags or hare. Upon seeing this decision, Elmer must decide whether he too will hunt stags or hares. The payoffs associated with their choices are presented at the end of each path. For example, if Yosemite chooses stag, but Elmer chooses hare, then Yosemite gets a payoff of zero, while Elmer gets one. In this story, stag is valuable only when both players hunt together. Notice the payoffs jump to two each if both of them choose to hunt stag.

Strategy for strategic situations

Once we’ve specified the strategic situation, we can look at possible strategies. Put simply, strategies are decision rules that players can use in a given strategic situation. In game theory, a complete strategy specifies a response at every information set. It accounts for every contingency, even if the decision node is unlikely to materialise in game.

In the example above, Yosemite has two strategies to choose from: Stag or Hunt. Elmer, by contrast, has four strategies to choose from: (1) Always choose stag; (2) Always choose hare; (3) Choose the opposite of Yosemite – hare if stag, and stag if hare; and (4) Choose the same as Yosemite – stag if stag, and hare if hare.

Possibility, permutation, and edge

In games like chess, specifying strategies in a game theoretic sense is impossible. There are just too many permutations and possibilities. Human players have to rely on their experience, knowing and intuition to sample a manageable set of strategies to select their preferred course of action. Introductory game theory, by contrast, focuses on a few options and permutations. In truth, though, there are probably infinite options to consider in life and business. For better and worse, we have no choice but to simplify the game into manageable components. Game theory is as much an art as it is a social science. Those that know how to scope, simplify, and focus will enjoy an edge in decision-making.

Information, history and recall

When specifying an extensive form game, we must consider whether it’s a game with perfect or imperfect information.

Perfect and imperfect information

If an extensive form game has perfect information, then players know the decisions that everyone has made prior to their turn. That is, they have a full account of the game’s history, and have perfect recall of everything that’s taken place. Sometimes, however, a player must make a choice at a decision node without knowledge of previous decisions. That is, due to imperfect information, players cannot tell which decision node they’re at. Imperfect information, in this sense, is a type of uncertainty.

Information sets

We use information sets to describe the group of nodes that a player cannot distinguish between. That is, the player knows which information set he is on, but not which decision node. To specify an information set, some textbooks may draw a dotted line between decision nodes. Others may draw a bubble around them. The decision tree below, for example, is a game of imperfect information. Elmer cannot tell which decision node he is at after Yosemite has made a decision. We represent this uncertainty with a dotted bubble.

Example of extensive game with imperfect information

Singleton

A singleton is an information set with a single decision node. If a player is on a singleton, she must know the decision node and which part of the game she is on. An extensive form game with perfect information will comprise only of singletons (as in our very first example). If one or more information sets are not singletons, then we have an extensive form game with imperfect information.

Normal or strategic form (simultaneous) games

Strategic form games, known also as normal form games, describe strategic situations in which players take their actions simultaneously. Rock-paper-scissors, for example, is a classic normal form game. We tend to describe simultaneous games in a table. The 2 x 2 table below, for example, is a simultaneous version of the Stag-Hunt game we introduced previously. In this game, Yosemite and Elmer have two strategies to choose from: 1) Stag; and 2) Hare. It follows that there are four possible strategic profiles (or combinations of player strategies) and associated payoffs. For example, if Yosemite chooses Hare, but Elmer chooses Stag, then Yosemite enjoys a payoff of one, while Elmer gets a payoff of zero.

Example of a strategic form game (Stag Hunt)

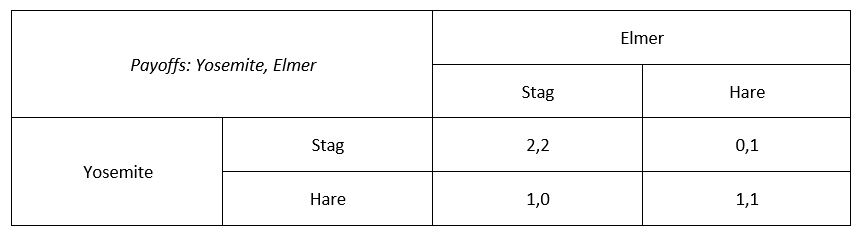
Transposition

Simultaneous games are sometimes comparable to sequential games with imperfect information. Intuitively, let’s say you must decide after your opponent has moved. If you don’t know what action she took, is it any different to moving at the same time? In this way, the simultaneous Stag-Hunt game is strategically equivalent to the sequential Stag-Hunt game with imperfect information. What matters in decision-making is not always the move order, but the availability of information. Sometimes, we can switch sequences without affecting the game because the information between players haven’t changed.